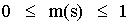4.
|
Чтобы измерить количество информации, содержащееся в сообщении
или сигнале, можно воспользоваться так называемой аддитивной
мерой Хартли. В соответствии с этой мерой количество информации
измеряется в двоичных единицах - битах.
|
|
5.
|
Введем понятия глубины сообщения и длины сообщения.
|
|
6.
|
Глубина сообщения q - количество различных элементов
(символов, знаков), принятых для представления сообщений. В каждый момент
времени реализуется только один какой-либо элемент.
Например, если сообщение представляется символами - буквами русского
алфавита, то q = 32 (для простоты буква ё во внимание не
принимается), английского - q = 26. Если сообщение -
десятичные числа, то q = 10 (десятичные цифры - элементы -
0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
|
|
7.
|
Длина сообщения n - количество позиций, необходимых и достаточных
для представления сообщений заданной величины.
Если символы сообщения - цифры, то сами сообщения - числа и их
последовательности.
Далее в настоящей книге понятие глубины сообщения будет трансформировано
в понятиеоснования системы счисления.
|
|
8.
|
При заданных глубине и длине сообщения количество всех возможных
сообщений (N), которое можно представить:
Например, всего трехбуквенных русских слов
N = 323 = 32768. Заметим, что
в это количество включены и "совершенно невозможные" слова,
например "ааа" или "ььы", но, подчеркнем, что при описываемом подходе
смысл (семантика) сообщения не рассматривается.
Другой пример. Трехзначных десятичных чисел всего
N = 103 = 1000.
|
|
9.
|
Величина N не удобна для оценки информационной емкости. Определим
логарифмическую меру, позволяющую вычислять количество
информации в битах. Такую информационную емкость (I) называют
мерой Хартли:
|
I = log2 N = n · log2 q
|
(2.2)
|
Для трехбуквенных русских слов
I = 3 · log2 32 = 15.
|
|
10.
|
Значение b = log2 q
- количество двоичных разрядов для кодирования (представления)
одного элемента. Это значение не может быть дробным, поэтому более точно:
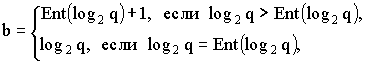
| (2.3)
|
где Ent(...) означает целую часть числа.
|
|
11.
|
Итак, 1 бит информации соответствует одному элементарному событию,
которое может произойти или не произойти. Такая мера количества информации
удобна тем, что она позволяет оперировать мерой как числом.
Количество информации при этом эквивалентно количеству двоичных символов
0 или 1.
|
|
12.
|
При наличии нескольких источников информации общее количество информации
равно
|
I = I1 + I2 + ... + Ik =
|
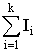
| (2.4)
|
Здесь I i - количество информации от источника i.
Всего источников - k.
|
|
13.
|
Логарифмическая мера информации позволяет измерить количество
информации и используется на практике.
В качестве примера рассмотрим следующую задачу.
|
|
14.
|
Необходимо определить, какое количество информации в битах содержит
книга, написанная на русском языке, содержащая 200 страниц
(каждая страница содержит приблизительно 2000 символов).
Для решения воспользуемся мерой Хартли
I = n · log2 q = 200 · 2000 · log2 32 = 2000000 бит.
Здесь n - длина сообщения в знаках:
n = 200 страниц · 2000 знаков/страница = 400000 знаков.
Итак, книга содержит около 2-х мегабит (Мбит) информации.
|
|
15.
|
В статистической теории информации Шеннона вводится
более общая мера количества информации, в соответствии с которой
рассматривается не само событие, а информация о нем.
(Напомним, что в теории информации под информацией понимаются
дополнительные сведения о событии.)
|
|
16.
|
Во введении к главе были приведены несколько примеров сообщений,
которые описывали состояние физической системы.
Очевидно, если бы состояние этой системы было известно заранее,
то не имело бы смысла передавать сообщение:
оно не имело бы никакой информации. Сообщение приобретает смысл
только тогда, когда состояние системы заранее неизвестно,
обладает какой-то степенью неопределенности.
Очевидно, сообщение, выясняющее для нас состояние такой системы,
будет тем богаче и содержательнее, чем больше была неопределенность
системы до этого сообщения (априори).
|
|
17.
|
Возникает естественный вопрос: что значит "большая" или "меньшая"
степень неопределенности и как ее можно измерить?
|
|
18.
|
Чтобы уяснить себе этот вопрос, сравним между собой две
физические системы, каждой из которых присуща некоторая неопределенность.
В качестве первой системы (обозначим ее А) возьмем монету,
которая подбрасывается и может случайным образом выпасть
той или иной стороной, то есть оказаться в одном из двух состояний:
А1 - "орел";
А2 - "решка".
|
В качестве второй системы (пусть будет В) возьмем игральный кубик,
который тоже подбрасывается и может оказаться в одном из шести состояний:
В1 - выпала единица;
В2 - выпала двойка;
. . .
В6 - выпала шестерка.
|
|
|
19.
|
Какая из этих систем обладает большей неопределенностью?
Очевидно, вторая, так как она отличается большим разнообразием
возможных состояний. С первого взгляда может показаться,
что все дело в числе состояний: у первой системы их два,
а у второй - шесть. Однако степень неопределенности зависит не
только от числа состояний, но и от их вероятностей.
Здесь под вероятностью появления какого-либо состояния понимается
величина, равная частоте (или средней частоте) появления:
отношению числа благоприятных исходов (появления события)
к общему количеству состояний.
|
|
20.
|
Чтобы убедиться в том, что степень неопределенности зависит
от вероятности появления события, рассмотрим третью систему С,
у которой, как и у системы А, два возможных состояния.
Пусть системой С будет техническое устройство, которое имеет два
возможных состояния:
С1 - устройство исправно;
С2 - устройство отказало.
|
Если вероятности этих двух состояний одинаковы (по 0,5 или 50%),
то степень неопределенности системы С такая же, как системы А (монета).
|
|
21.
|
Теперь представим себе, что состояния С1 и С2
неравновероятны, например, вероятность первого - 0,99 (99%),
а вероятность второго - 0,01 (1%).
Очевидно, степень неопределенности такой системы будет гораздо меньше,
чем в первом случае: ведь мы почти уверены, что устройство будет исправно.
А если состояние С1 будет совершенно достоверно (то есть иметь
вероятность 1), то, очевидно, система С вообще никакой неопределенностью
обладать не будет.
|
|
22.
|
Таким образом, мы убедились, что степень неопределенности физической
системы зависит не только от числа состояний, но и от того, как
распределены вероятности между состояниями.
|
|
23.
|
В теории информации в качестве меры неопределенности системы принята
так называемая энтропия.
Если система А имеет n возможных состояний
причем вероятности этих состояний равны соответственно
|
|
p1 , p2 , ..., pn;
p1 + p2 + ... + pn = 1,
|
|
то энтропией системы А называется величина:
|
H(A) = -(p1 · log2 p1 + p2 · log p2 + ... + pn · log pn),
| (2.5)
|
или
|
| H(A) = -
| 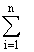
| pi · log q,
| (2.6)
|
то есть сумма произведений вероятностей состояний на логарифмы
этих вероятностей, взятая с обратным знаком (обратный знак берется
просто для того, чтобы энтропия была неотрицательной).
|
|
24.
|
Логарифм в формуле (2.6) может быть взят при любом основании.
Обычно логарифм берется по основанию 2. Тогда говорят, что энтропия
измеряется в двоичных единицах (битах):
|
| 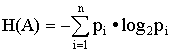
| (2.7)
|
|
|
25.
|
Один бит - это энтропия простейшей физической системы,
которая может быть только в одном из двух состояний,
причем эти состояния равновероятны.
Действительно, пусть система А обладает двумя состояниями
А1 и А2 с вероятностями p1 = 0,5
и p2 = 0,5. Согласно формуле (2.7), энтропия
такой системы равна
|
|
H(A) = - (0,5·log2 0,5 + 0,5·log2 0,5) = 1,
|
|
то есть одному биту.
|
|
26.
|
В классической теории информации количество информации,
заключенной в сообщении, измеряется уменьшением энтропии системы
под действием этого сообщения. Пусть, например, до поступления
сообщения энтропия системы была равна двум битам, а после него
стала равной одному биту. Из этого мы заключаем, что информация,
заключенная в сообщении, равна одному биту.
|
|
27.
|
Понятию "информация в битах" можно дать очень наглядное истолкование:
она равна числу ответов "да" и "нет" на разумно поставленные вопросы,
с помощью которых можно получить ту же информацию.
Пусть, например, система А может иметь два равновероятных состояния:
А1 и А2. Тогда полное выяснение состояния этой
системы несет информацию один бит, и, значит, можно ее получить в
результате ответа на один вопрос. Действительно, задав один-единственный
вопрос: "Находится ли система в состоянии А1?"
и получив на него ответ "да" или "нет", мы полностью выясним состояние
системы.
|
|
28.
|
Возьмем другой пример. Имеется шахматная доска, на одну из клеток
которой поставлена фигура (слон). Предположим, что все клетки выбираются
с одинаковой вероятностью.
Определим информацию, заключенную в сообщении о том, где стоит слон.
У системы А (слон) 64 равновероятных состояния; ее энтропия равна:
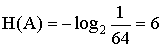
Значит, сообщение, полностью устраняющее неопределенность состояния системы
(указание, где стоит слон), должно содержать ровно шесть битов информации.
А из этого следует, что положение слона можно точно выяснить с помощью не
более чем шести вопросов. (Предлагаем читателю в качестве упражнения
самостоятельно сформулировать эти шесть вопросов.)
|
|
29.
|
Энтропия обладает следующими свойствами:
а) энтропия всегда неотрицательна, так как значения вероятностей выражаются
величинами, не превосходящими единицу, а их логарифмы - отрицательными
числами или нулем, так что члены суммы (2.7) неотрицательны;
б) если pi = 1 (а все остальные pj = 0, j = 1, ..., (n-1)),
то Н(А) = 0. Это тот случай, когда об опыте или величине все известно
заранее и результат не дает новую информацию;
в) H(A) = Hmax при p1 = p2 = ... = pn = 1 / n,
при этом
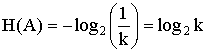
| ;
|
г) энтропия системы, состоящей из двух подсистем А и В
(состояния системы образуются совместной реализацией объектов А и В), то есть:
Н(АВ) = Н(А) + Н(В).
|
|
30.
|
Если события равновероятны и статистически независимы, то оценки
количества информации, по Хартли и Шеннону, совпадают.
Это свидетельствует о полном использовании информационной емкости системы.
В случае неравных вероятностей количество информации, по Шеннону,
меньше информационной емкости системы.
Количество информации только тогда равно энтропии, когда
неопределенность ситуации снимается полностью. В общем случае
нужно считать, что количество информации есть уменьшение энтропии
вследствие опыта или какого-либо другого акта познания.
Если неопределенность снимается полностью, то информация равна энтропии:
I = H.
В случае неполного разрешения имеет место частичная информация,
являющаяся разностью между начальной (H0) и конечной
(H1) энтропией:
I = H0 - H1.
|
|
31.
|
Таковы в самых общих чертах принципиальные основы классической теории
информации. Она дает полезный аппарат, позволяющий решать ряд
важных практических задач (например в теории связи при кодировании
речи или изображений). Однако этот аппарат не универсальный,
и множество ситуаций не укладывается в шенноновскую модель.
|
|
32.
|
Отметим, что далеко не всегда можно заранее (до сообщения)
установить перечень возможных состояний системы и вычислить их вероятности.
Например, вряд ли можно численно оценить вероятность того,
что в нашей солнечной системе существует еще одна - десятая - планета.
Тем не менее, с точки зрения обычного здравого смысла (а не нарушать
его - естественное требование к теории) ясно, что сообщение об
открытии новой планеты должно нести очень большую информацию,
но оценить ее в битах не удается.
|
|
33.
|
Другой пример. Допустим, что система радиолокационных станций
ведет наблюдение за воздушным пространством с целью обнаружения самолета
противника. Система А, за которой ведется наблюдение, может быть
в одном из двух состояний:
А1 - противник есть;
А2 - противника нет.
|
Выяснение, в каком из них именно она находится, в рамках
классической теории в лучшем случае принесло бы нам информацию
один бит, равную информации о том, какой стороной вверх упала монета.
Совершенно ясно, что по своей важности первое сообщение несравненно
больше второго, но оценить его в рамках классической теории невозможно.
|
|
34.
|
Таким образом, основным недостатком классической теории информации,
ограничивающим ее применение, является то, что она, занимаясь только
формальной ("знаковой" или "буквенной") стороной сообщений, оставляет
в стороне их ценность и важность, вообще -
содержание.
|
|
35.
|
Естественно, возникают попытки создания методов количественной
оценки информации, которые бы учитывали ее смысловое содержание.
Эта ветвь науки некоторыми учеными называется теорией семантической
(смысловой) информации. Укажем некоторые ее подходы.
|
|
36.
|
Предположим, что поступает сообщение S, нужное нам для того, чтобы
в соответствии с его содержанием организовать свою дальнейшую деятельность.
Например, мы слушаем по радио прогноз погоды с тем, чтобы решить:
как одеться для предстоящей рыбалки? Одним словом, мы собираемся
предпринять какое-то мероприятие или совокупность мероприятий (короче -
"операцию"), а сообщение касается тех условий, в которых она будет проходить.
|
|
37.
|
В этом случае, естественно, нужно оценивать информацию, содержащуюся
в сообщении, по увеличению эффективности той операции, в интересах
которой поступает информация. Предположим, что эффективность операции
может быть оценена численно с помощью какого-то критерия W, и мы хотим
эту величину сделать максимальной. Пусть без сообщения S эффективность
операции оценивается величиной Ws. Естественно предположить,
что приращение эффективности
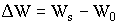
в какой-то мере характеризует ценность и важность полученного сообщения.
|
|
38.
|
Пусть, например, операция состоит в подборе ассортимента товаров
для торговой точки, а сообщение S касается покупательского спроса на
отдельные виды товаров в данном районе. В качестве критерия эффективности
W рассматривается вырученная прибыль. Тогда ценность информации, заключенной
в сообщении S, можно оценить разницей (Ws - W0),
где W0 - прибыль, которую мы получили бы без сообщения S,
Ws - прибыль, которую мы получили с учетом сообщения S.
|
|
39.
|
Выделим в качестве семантических мер наиболее распространенные в теории
содержательность и целесообразность.
|
|
40.
|
Содержательность сообщения (события) S выражается через функцию
меры m(s) - содержательности его отрицания. Оценка содержательности основана
на математической логике, в которой логические функции истинности m(s)
и ложности 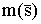 имеют формальное
сходство с функциями вероятностей события p(s) и антисобытия q(s)
в теории вероятностей. имеют формальное
сходство с функциями вероятностей события p(s) и антисобытия q(s)
в теории вероятностей.
|
|
41.
|
Как и вероятность, содержательность события изменяется в пределах
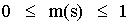
|
|
42.
|
Мера целесообразности информации определяется как изменение
вероятности достижения цели при получении дополнительной информации.
Полученная информация может быть пустой, то есть не изменять вероятности
достижения цели, и в этом случае ее мера равна нулю.
В других случаях полученная информация может изменять положение дела
в худшую сторону, то есть уменьшать вероятность достижения цели,
и тогда она будет дезинформацией, которая измеряется
отрицательным значением количества информации. Наконец, в благоприятном
случае получается добротная информация, которая увеличивает вероятность
достижения цели и измеряется положительной величиной количества информации.
|
|
43.
|
Мера целесообразности в общем виде может быть аналитически выражена
в виде соотношения
|
|
I = log2 p(s) - log2 p0,
| (2.8)
|
где p(s) и p0 - конечная (после получения сообщения S) и начальная
(до получения сообщения) вероятности достижения цели.
|
|
44.
|
Конечно, этими характеристиками количество информации
оценивается косвенно. Такой косвенный способ учета содержания
информации в некоторых случаях, безусловно, правомочен
и является некоторым шагом вперед, преодолевающим ограниченность
классической теории. Однако и эта постановка вопроса пригодна
далеко не для всех ситуаций. Она основана на предположении,
что информация, содержащаяся в сообщении, будет использована в
интересах какой-то вполне определенной операции и только в них.
На практике же часто встречаются случаи, когда информация
вовсе не предназначена для обслуживания какой-либо определенной
операции, а просто расширяет объем наших сведений о некотором классе
явлений, причем совершенно не известно, когда и как эта информация
может быть использована (например информация, полученная
фотографированием Марса).
|
|
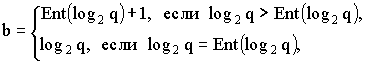
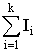
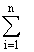
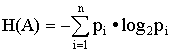
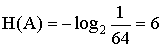
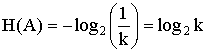
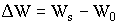
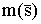 имеют формальное
сходство с функциями вероятностей события p(s) и антисобытия q(s)
в теории вероятностей.
имеют формальное
сходство с функциями вероятностей события p(s) и антисобытия q(s)
в теории вероятностей.