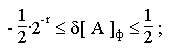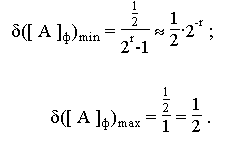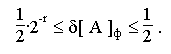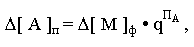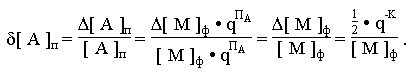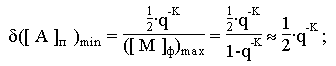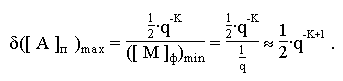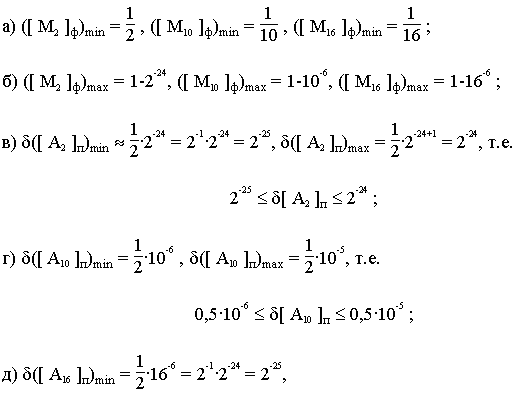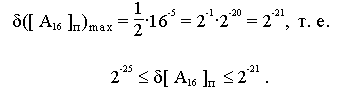|
ГЛАВА 7. ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ В ЯЧЕЙКАХ ПАМЯТИ |
|---|
ВВЕДЕНИЕ |
|---|
ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ |
|---|
| 6. |
Число 0,00234 можно записать так: 234 · 10-5, или 0,002 (с округлением), или 2,34 · 10-3 и т.д. Разнообразие форм в записи одного числа может послужить причиной затруднений для работы компьютера.
Во избежание этого нужно либо создать специальные алгоритмы "узнавания"
числа, либо указывать каждый раз форму его записи. Очевидно, второй путь
проще.
| |||
| 7. |
Существует две формы записи чисел: естественная и нормальная. При естественной форме число записывается в естественном, натуральном виде, например, 12560 - целое число; 0,0035 - правильная дробь; 4,67 - неправильная дробь. При нормальной форме запись одного числа может принимать разный вид в зависимости от ограничений, накладываемых на ее форму. Например, число 12560 можно записать так: 12560 = 1,256 · 104 = 0,1256 · 105 = 125600 · 10-1 и т. д. | |||
| 8. |
Машинное изображение числа - представление числа Aq в разрядной сетке ЭВМ (в ячейке памяти). Условно обозначим машинное изображение числа символом [A]. Тогда справедливо соотношение
где KA - коэффициент, величина которого зависит от формы
представления числа в ЭВМ.
|
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ С ФИКСИРОВАННОЙ ТОЧКОЙ |
|---|
| 9. |
Естественная форма представления числа в ЭВМ характеризуется тем, что положение его разрядов в машинном изображении остается всегда постоянным независимо от величины самого числа. Другое название этой формы - представление с фиксированной точкой - ФТ (запятой) (имеется в виду запятая, отделяющая целую часть от дробной). | |||||
| 10. |
Чтобы упростить функционирование компьютера, необходимо ограничить входную информацию какой-то одной областью чисел, что позволит определить KA. Например, если на вход вычислительной машины поступают только правильные дроби, то
где [A]ф - машинное изображение числа с ФТ.
Тогда число А будет представлено в виде A = [A]ф · KA.
| |||||
| 11. |
Величина KA определяет тот факт, что в машинном изображении точка (запятая) всегда стоит перед старшим разрядом дроби. Следовательно, можно хранить только дробную часть числа, а в разряде целой части писать дополнительную информацию. | |||||
| 12. |
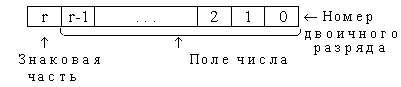
Так как числа бывают положительные и отрицательные, то формат (разрядная сетка) машинного изображения разбивается на знаковую часть и поле числа (рис. 7.1).
Рис. 7.1. Представление чисел с ФТ (правильные дроби)
В знаковую часть записывается информация о знаке. Примем, что знак
положительного числа "+" изображается символом 0, а знак отрицательного
числа "-" изображается символом 1.
| |||||
| 13. |
Если на вход ЭВМ поступают целые числа, то в разрядной сетке один разряд отводится под знак числа, последующие разряды образуют поле числа (рис. 7.2).
Рис. 7.2. Представление чисел с ФТ (целые числа)
Если числа представлены в двоичной системе счисления, q = 2, то
диапазон представления чисел в этом случае:
Заметим, что нумерация разрядов различна: для чисел с ФТ
(правильные дроби) - слева направо, для чисел с ФТ (целые) справа налево.
| |||||
| 14. |
Если q 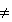 2,
то для каждой цифры Aq требуется только (S) двоичных разрядов
(q=8, S=3; q=10, S=4 ...). 2,
то для каждой цифры Aq требуется только (S) двоичных разрядов
(q=8, S=3; q=10, S=4 ...).
Чтобы определить S, зная q, можно воспользоваться следующей зависимостью:
где Ent(*) означает целую часть числа.
Всего в r-разрядной двоичной ячейке может разместиться
Если частное Значение Y можно найти из соотношения
где Res(*) означает остаток от деления. Итак, старшая цифра целого числа при ее неполном (Y<S) представлении, всегда несколько (Y) единиц. Ее количественное значение (2Y-1).
Пример 1. Пусть r = 16. Определить машинные изображения двоичного, десятичного и шестнадцатеричного чисел, то есть значения [(A2)max]Ф, [(А10)max]Ф, [(А16)max]Ф. Решение. а) q = 2.
Изображения чисел:
В обоих случаях
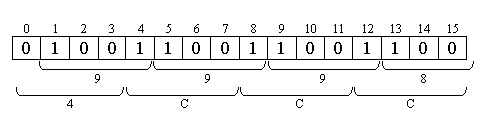
[(A2)max]Ф = 7FFF; б) q = 10. Запишем максимальное десятичное число в 16-разрядную двоичную ячейку. Для целых чисел:
Для правильных дробей:
в) q = 16. Для правильных дробей:
Для целых:
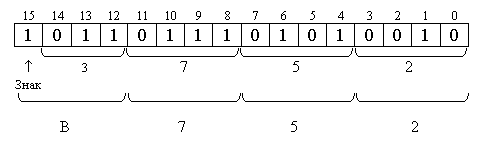
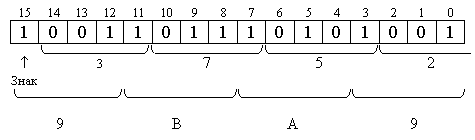
Пример 2. Представить число -37,5310 в форме с фиксированной точкой в шестнадцатиразрядной ячейке. Рассмотреть варианты q = 2; 10; 16. Решение. Так как числа с фиксированной точкой представляются либо как правильные дроби, либо как целые, будем рассматривать оба варианта. А. Целые числа.
В. Числа - правильные дроби.
| |||||
| 15. |
Если | А | > Amax, то число не размещается в разрядной сетке (ячейке). Попытка все же его записать приводит к ошибке. Соответствующая ситуация носит название "переполнение". При выполнении в компьютере арифметических операций результат автоматически проверяется на переполнение. |
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ С ПЛАВАЮЩЕЙ ТОЧКОЙ |
|---|
| 16. |
В нормальной форме, или в форме с плавающей точкой - ПТ (запятой), число записывается в виде:
где | |||||||
| 17. |
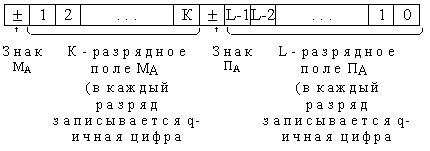
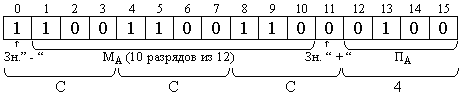
Ниже приведен формат изображения чисел с ПТ:
Знак МA - знак числа. Мантисса должна быть нормализованной,
т.е. удовлетворять условию:
Во время арифметических операций числа с ПТ автоматически нормализуются.
Это позволяет поддерживать высокую точность вычислений. Заметим, что
условия нормализации обеспечивают ненулевую старшую цифру мантиссы.
| |||||||
| 18. |
Порядок - целое число (нумерация разрядов на рисунке справа налево: младшая значащая цифра порядка - справа). Он изменяется в пределах
| |||||||
| 19. |
Представление чисел с ПТ обеспечивает диапазон
Минимальное, отличное от нуля, положительное число:
Максимальное число:
| |||||||
| 20. |
Пример 3.
Пример 4.
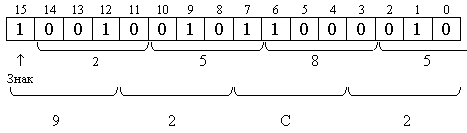
Пример 5. Компьютер имеет 16-разрядную ячейку памяти. Для чисел с ПТ 10 двоичных разрядов отводится для изображения мантиссы, 4 - для изображения порядка. Система счисления 2, 10, 16. Представить изображение числа - 9,610. Результат записать шестнадцатеричными цифрами (компактная форма). Решение. Представим разрядную сетку (r = 16):
а) q = 2: A10 = -9,6 = -1001,1001110012 = - 0,100110011001·24. MA = - 0,100110011001 ПA = 410 = 1002
[A2]П = CCC4; б) q = 10. A10 = - 9,6 · 101.
[A10]П = CB01; в) q = 16. A16 = - 9,99 = - 0,999 · 161.
[A16]П = CCC1.
|
ПОГРЕШНОСТИ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ |
|---|
| 21. |
Представление числовой информации в компьютере, как правило, влечет за собой появление погрешностей (ошибок), величина которых зависит от формы представления чисел и от длины разрядной сетки (ячейки памяти). | ||||||||||||||||||||||
| 22. |
Абсолютная погрешность представления - разность между истинным значением входной величины А и ее значением, полученным из машинного изображения AM, т.е.:
| ||||||||||||||||||||||
| 23. |
Относительная погрешность представления - величина
| ||||||||||||||||||||||
| 24. |
Входные величины, независимо от количества значащих цифр, могут содержать грубые ошибки, возникающие из-за опечаток, некорректной постановки задачи или отсутствия более полной информации. Например, часто принимают 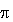 = 3,14.
Однако эта же величина может быть получена с более высокой точностью
(800 знаков после запятой и более). Если принять, что точное значение = 3,14.
Однако эта же величина может быть получена с более высокой точностью
(800 знаков после запятой и более). Если принять, что точное значение
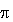 = 3,14159265, то
абсолютная погрешность равна = 3,14159265, то
абсолютная погрешность равна
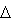 [ [
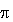 ] = 0,00159265. ] = 0,00159265.
Часто некоторая величина в одной системе счисления имеет конечное
значение, а в другой становится бесконечной величиной, например,
дробь 0,1 имеет конечное десятичное представление, но,
будучи переведенной в двоичную систему счисления, становится
бесконечной дробью 0,0001100110011... . Следовательно, при переводе
чисел из одной системы счисления в другую неизбежно возникают погрешности,
оценивать которые нетрудно, если известны истинные значения входных чисел.
| ||||||||||||||||||||||
| 25. |
Максимальная абсолютная погрешность для чисел с ФТ не превышает единицы младшего разряда:
Минимальная абсолютная погрешность равна нулю.
Средняя (усредненная) абсолютная погрешность
не превышает половины единицы младшего разряда. Эти величины будем
использовать в качестве основных:
Для двоичных (q = 2) чисел заданных форматами рис. 7.1 и 7.2:
| ||||||||||||||||||||||
| 26. |
Различают максимальную и минимальную относительные погрешности представления: а) для правильных дробей:
При q = 2:
При q = 2:
Таким образом
б) для целых чисел (q=2):
Итак,
Заметим, что точность представления одинакова для чисел с ФТ целых и
дробных. Кроме того, погрешности представления малых чисел могут быть очень
значительными.
| ||||||||||||||||||||||
| 27. |
Абсолютная ошибка представления чисел с ПТ равна
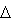 [ M ]ф =
( 1/2 )·q-K, т.к. мантисса представляется числом с ФТ -
правильной дробью. [ M ]ф =
( 1/2 )·q-K, т.к. мантисса представляется числом с ФТ -
правильной дробью.
Следовательно, абсолютная погрешность зависит от порядка числа:
она минимальна при наибольшем отрицательном порядке -Пmax и
максимальна при наибольшем положительном +Пmax.
| ||||||||||||||||||||||
| 28. |
Относительная погрешность представления чисел с ПТ не зависит от порядка
Определим диапазон изменения относительной ошибки:
Таким образом,
т.е. точность представления чисел с ПТ изменяется в незначительных пределах
и не зависит от величины числа.
| ||||||||||||||||||||||
| 29. |
Пример 6. Компьютер имеет 32-разрядную ячейку памяти, в которую записываются числа с ПТ. Под мантиссу отводится 24 двоичных разряда, под порядок - 6. Определить точность представления для двоичных, десятичных и шестнадцатеричных чисел (q = 2, 10, 16). Решение.
|
КРАТКО О ГЛАВНОМ |
|---|
| 1. |
Память компьютера - набор адресуемых ячеек. В ячейках хранятся двоичные многоразрядные числа. Основные способы представления чисел - представление с фиксированной и плавающей точкой (запятой). | |
| 2. |
Числа с фиксированной точкой (запятой) используются для представления или целых чисел, или правильных дробей. | |
| 3. |
Числа с плавающей точкой представляются мантиссой и порядком. Мантисса должна быть нормализованной. | |
| 4. |
Формы представления чисел характеризуются диапазоном представления, абсолютной и относительной погрешностью. |


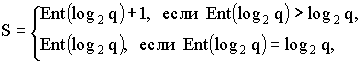
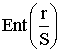 полных цифр q-ичного числа.
полных цифр q-ичного числа.
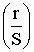 имеет дробную часть, то для целых чисел старшая цифра должна размещаться
в двоичных разрядах, число которых Y меньше S:
имеет дробную часть, то для целых чисел старшая цифра должна размещаться
в двоичных разрядах, число которых Y меньше S:
 .
.

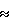 1.
1.

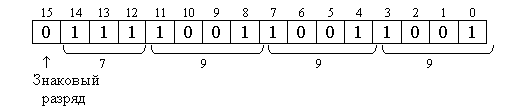
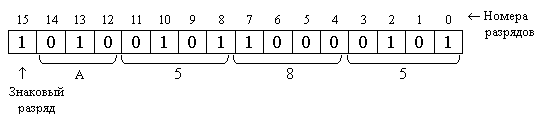

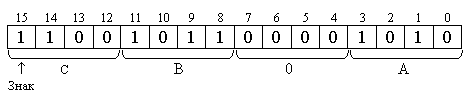

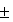 MA
- мантисса числа со знаком;
MA
- мантисса числа со знаком;
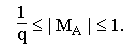
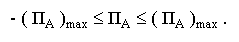
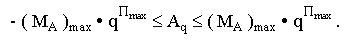
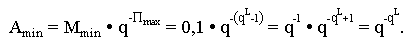
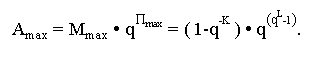

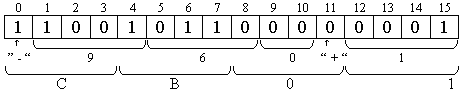
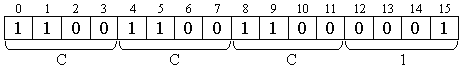
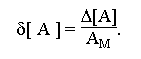
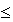 1 - для целых чисел и
1 - для целых чисел и
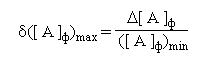
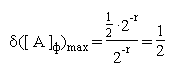
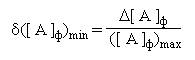
 (при большом r).
(при большом r).