|
ГЛАВА 1. ЛОГИКА И ЭЛЕМЕНТЫ СХЕМОТЕХНИКИ |
|---|
АЛГЕБРА ЛОГИКИ |
|---|
| 1. |
Логика - наука, изучающая методы доказательств и опровержений, то есть методы установления истинности или ложности одних высказываний (утверждений, суждений) на основе истинности или ложности других высказываний. | |
| 2. |
Математическая логика - это современная форма логики, которая полностью опирается на формальные математические методы. Частью математической логики является алгебра логики - раздел, изучающий строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов. | |
| 3. |
Алгебру логики иногда называют алгеброй Буля, или булевой алгеброй, по имени ее создателя - Джоржа Буля - английского математика (кстати, отца Этель Л. Войнич, написавшей "Овод"). Основные результаты теории были сформулированы им в книге "Исследование законов мышления", изданной в 1854 году. Во введении Буль писал, что назначение трактата - исследовать основные законы тех операций ума, посредством которых производится рассуждение, выразить их на символическом языке некоторого исчисления и на этой основе установить науку логику и построить ее метод. Глава содержит краткие сведения о логических переменных, основных операциях, построении и преобразовании логических функций. |
НАЧАЛЬНЫЕ СВЕДЕНИЯ |
|---|
| 4. |
Основным объектом изучения математической логики являются элементарные высказывания. Под термином "высказывание" мы будем понимать повествовательное предложение. При этом нас будет интересовать не построение: подлежащее - сказуемое - дополнение, а характерные свойства рассматриваемых образований: являются они истинными или ложными. Высказывания отличаются от других языковых образований тем, что мы можем присвоить им определенное значение истинности - "истина", если они истинны, значение "ложь", если они ложны. При этом мы исходим из "принципа исключенного третьего", или "третьего не дано", который состоит в том, что каждое высказывание или истинно, или ложно, и других возможностей нет. Ситуация, когда ни истинно, ни ложно, была бы и в обычном смысле неразрешимой. Этот принцип называют принципом двузначности. Все научные знания (законы и явления физики, химии и биологии, математические теоремы и т.д.), события повседневной жизни, ситуации, возникающие в процессах управления, формулируются в виде высказываний. Примерами указанных высказываний являются: "35 делится на 7", "Москва - столица России". Все они имеют значение истинности "истина". Следующие высказывания имеют значение истинности "ложь": "Мышь больше слона", "Молодые лошади называются щенятами", "6 больше 8". Повелительные ("Войдите, пожалуйста!"), вопросительные ("Знаешь ли ты информатику?") и бессмысленные предложения не являются высказываниями. |
|
|---|---|---|
| 5. |
Если логика имеет дело со смыслом высказываний, то в алгебре логики работают с формулами. Любое элементарное высказывание обозначается малой буквой латинского алфавита (в нашем повествовании - х i ) , совершенно так же, как в элементарной алгебре обозначаются величины, когда мы абстрагируемся от того, какие именно предметы изучаются, нас интересует только их количество и соотношение между ними. Поскольку высказывание может принимать одно из двух значений, то говорят о "переменных высказываниях". Это означает, что рассматривается не только конкретно определенное высказывание хi , но также некоторая логическая переменная х i , которую можно использовать для обозначения произвольного высказывания. Замещение переменной конкретным высказыванием означает предоставления одного из значений "истина" или "ложь". |
|
| 6. |
Итак, в алгебре логики в каждом высказывании мы будем отвлекаться от всех особенностей высказывания, кроме одного - истинно оно или ложно. Истинное высказывание условно обозначается единицей (если x1 - высказывание " 35 делится на 7", то x1 = 1), а ложное - нулем (если x2 - высказывание "мышь больше слона", то x2 = 0). | |
| 7. |
Таким образом, диапазон изменения переменного - xi в алгебре логики существенно меньше, чем изменение переменного в элементарной алгебре: оно принимает только одно из двух значений - или 1, или 0. | |
| 8. |
Из элементарных высказываний с помощью логических связок " и", "или", "не", "если : то" и других (логических операций) строятся сложные высказывания - формулы (или функции ) алгебры логики. Способы построения новых высказываний из заданных с помощью логических связок, их преобразования и установления истинности изучаются в логике высказываний с помощью алгебраических методов. | |
| 9. |
Сущность алгебраического подхода к логике поясним на примере элементарной алгебры - алгебры арифметики. Основные объекты алгебры арифметики - выражения (формулы), состоящие из букв, знаков операций и скобок. С формулами производят процедуры двух типов: вычисления и преобразования. Вычисления - вместо букв подставляют числа, знаки указывают действия, а скобки их порядок. Каждая формула задает функцию. Переменные - буквы формулы. Преобразование формулы происходит так: исходная формула или ее часть F1 заменяется другой, в результате получается новая формула F2, которая эквивалентна F1 (т.е. при любых значениях аргументов F1 и F2 дают один и тот же результат). Преобразование выражений производится на основе законов арифметики, а также полученных из них соотношений типа (a + b) 2 = a 2 + 2ab + b 2 и т.п. По аналогии строится алгебра логики. Она рассматривает логические выражения как алгебраические, которые можно преобразовать по определенным правилам. Разница заключается в том, что в выражениях алгебры логики переменные являются логическими (0 и 1). Знаки операций обозначают логические операции (логические связки). | |
| 10. |
В логических задачах исходными данными являются суждения, подчас неожиданные и нередко весьма запутанные. Высказывания и связи между ними бывают иногда столь противоречивыми, что такие "твердые орешки" не под силу "раскусить" и вдумчивому математику. В данных случаях большую помощь может оказать ЭВМ как необходимый инструмент эффективного решения логических задач с многими переменными. В настоящее время нет ни одного языка программирования, который не включал бы логических операций. |
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ |
|---|
| 11. |
В алгебре логики основными (элементарными) операциями являются отрицание, логическое сложение (дизъюнкция), логическое умножение (конъюнкция), импликация, эквивалентность. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12. |
Отрицание. Операция отрицания соответствует в обычном языке частице не. Функция, получающаяся в результате применения операции отрицания к высказыванию x , обозначается так: 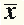 . Читается "
не икс". Заметим, что в математической логике до сих пор нет единых
обозначений, поэтому вместо . Читается "
не икс". Заметим, что в математической логике до сих пор нет единых
обозначений, поэтому вместо 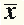 можно встретить и другие обозначения, смысл которых тот же самый, например,
можно встретить и другие обозначения, смысл которых тот же самый, например,
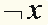 или или 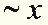 . .
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13. |
Новое сложное высказывание 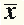 - ложно при условии, что высказывание x истинно и истинно при условии, что
x - ложно. Запишем эти зависимости в виде таблицы истинности
(формальное определение дадим позднее) для операции отрицания:
- ложно при условии, что высказывание x истинно и истинно при условии, что
x - ложно. Запишем эти зависимости в виде таблицы истинности
(формальное определение дадим позднее) для операции отрицания:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
| | 14.
| Пример 1. Обозначим суждение (высказывание) "Я иду в кино " через x 1, а суждение "Я достаю билеты в театр " через x 2 . Тогда в сложном суждении " Если я завтра достаю билеты в театр, то не иду в кино ( x 2 = 1, x 1 = 0), а если я не достану билеты в театр, то пойду в кино ( x 2 = 0, x 1 = 1)" высказывания x 1 и x 2 связаны между собой операцией отрицания: x 1 = 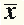 . .
| | 15.
| Логическое умножение (будем называть как в математической логике - конъюнкцией). Обозначается x1 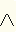 x 2 Другие обозначения:
x 1
·
x 2,
x 1& x 2.Читается "
икс один и икс два".
Это сложное суждение, которое истинно только в том случае, когда и суждение
x1, и суждение x
2 истинны. В остальных случаях сложное высказывание ложно.
Таблица истинности для конъюнкции (логического умножения):
x 2 Другие обозначения:
x 1
·
x 2,
x 1& x 2.Читается "
икс один и икс два".
Это сложное суждение, которое истинно только в том случае, когда и суждение
x1, и суждение x
2 истинны. В остальных случаях сложное высказывание ложно.
Таблица истинности для конъюнкции (логического умножения):
| |
|
| | 16.
| Пример 2 . Рассмотрим условия, необходимые для получения человеком водительских прав. Суждение " Человек получает права водителя" обозначим через y. Для получения прав необходимо получить положительное заключение медицинской комиссии о состоянии здоровья. Сформулируем высказывание " Человек здоров" и обозначим его x1. Кроме здоровья, надо еще сдать два экзамена: по вождению и по правилам дорожного движения (ПДД). Высказывания: x 2 - " Экзамен по вождению сдан успешно"; x 3 - " Экзамен по ПДД сдан успешно". В символической записи имеем: 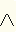 x 2
x 2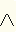 x 3(или
y =
x 1
x 2
x 3 ).
x 3(или
y =
x 1
x 2
x 3 ).
Суждение y будет истинным ( y = 1) только в том случае, если истинны все три суждения: x 1 = 1, x 2 = 1 и x 3 = 1. При всех других комбинациях y = 0, то есть высказывание y ложно: человек не получит прав водителя.
| | 17.
| Логическое сложение (дизъюнкция). Обозначается x 1 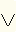 x 2 . Читается "икс один или икс два". Знак "
x 2 . Читается "икс один или икс два". Знак "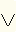 " взят из латинского языка, в котором есть союз "Vel", означающий
или то, или другое, или то и другое вместе.
Vel
более точно определяет суть логического сложения, чем русский союз или
, так как последний, кроме значения или то, или другое, или то и другое вместе
, имеет еще и другое значение - или только то, или только другое.
" взят из латинского языка, в котором есть союз "Vel", означающий
или то, или другое, или то и другое вместе.
Vel
более точно определяет суть логического сложения, чем русский союз или
, так как последний, кроме значения или то, или другое, или то и другое вместе
, имеет еще и другое значение - или только то, или только другое.
Логическое сложение выражает суждение (сложное высказывание), которое истинно в том случае, если хотя бы одно из суждений истинно.
| |
| Таблица истинности логического сложения:
| |
|
| | 18.
| Пример 3. Боря давно хотел иметь книгу "Основы информатики и вычислительной техники", где рассматриваются вопросы алгебры логики. Он попросил своих товарищей Андрея и Валерия, чтобы они обязательно купили для него эту книгу, если она им попадется. У Бориса будет книга (суждение y ) при выполнении равенства:
| |
| 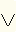 x 2,
x 2,
| |
| где x 1 - высказывание "Андрей купил книгу",
| |
| x 2 - высказывание "Валерий купил книгу".
| |
| Высказывание y = x 1 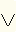 x 2,
не исключает случая, что книгу купят и Андрей, и Валерий.
x 2,
не исключает случая, что книгу купят и Андрей, и Валерий.
| | 19.
| Импликация. Обозначается x 1 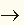 x 2
. Логически реализует связку естественной речи "
если : то". Импликация определяется следующим образом:
x 2
. Логически реализует связку естественной речи "
если : то". Импликация определяется следующим образом:
| |
|
| | 20.
| Например, в профессиональной речи следователь часто логически рассуждает примерно так: "Если кража произошла до полуночи, то наверняка это совершил Вольдемар". Нетрудно заметить, что два высказывания: x 1 - " Кража произошла до полуночи"и x 2 - " Вор - Вольдемар" связаны операцией импликации x 1 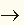 x 2 x 2
| |
| Данное умозаключение будет истинным, если при истинном x 1 истинно x 2 . Логическое выражение будет ложным, если при истинном x 1 оказывается ложным x 2.
| |
| Замечание. Если x 1 = 0 (высказывание - предположение ложно, или, говорят, ложная посылка), то x 2( следствие) может быть как истинным ("Вор - Вольдемар", x 2 =1), так и ложным ("Вор - не Вольдемар", x 2 = 0). Но логического смысла выражение не имеет.
| | 21.
| Данное положение вещей выражается с помощью поговорки " ex falso guod libet", или " из ложной посылки можно вывести всякое".
| |
| В обычной речи такие высказывания не имеют значения, поскольку выражения типа " Если кто-то сумасшедший, то 5 меньше 2" рассматриваются как бессмысленные. Это связано с тем, что в обычной речи предусматривается содержательная связь, причинные отношения между посылкой (причиной) x 1 и заключением (следствием) x 2, которые здесь не заданы. Такая содержательная связь не может быть описана с помощью логики высказываний.
| | 22.
| Эквивалентность . Эквивалентностью (или эквиваленцией) двух высказываний x 1 и x 2 называется новое высказывание, которое считается истинным, когда оба высказывания x 1 и x 2 либо одновременно истинны, либо одновременно ложны, и ложным - во всех остальных случаях.
| |
| Эквивалентность высказываний x 1 и x 2 обозначается символом x 1  x 2 (или x 1 =
x 2, или x 1
x 2 (или x 1 =
x 2, или x 1
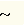 x 2), читается "
для того, чтобы x 1, необходимо и достаточно, чтобы
x 2" или " x 1
тогда и только тогда, когда
x 2". Высказывания
x 1 и x 2 называются членами эквивалентности. x 2), читается "
для того, чтобы x 1, необходимо и достаточно, чтобы
x 2" или " x 1
тогда и только тогда, когда
x 2". Высказывания
x 1 и x 2 называются членами эквивалентности.
| | 23.
| Логические значения операции эквивалентности описываются следующей таблицей истинности.
| |
|
| | 24.
| Например, эквивалентность " Треугольник SPQ с вершиной S и основанием PQ равнобедренный тогда и только тогда, когда угол P равен углу Q " является истинной, так как высказывания " Треугольник SPQ с вершиной S и основанием PQ равнобедренный" и " В треугольнике SPQ с вершиной S и основанием PQ угол P равен углу Q " либо одновременно истинны, либо одновременно ложны.
| | 25.
| Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.
| | 26.
| Итак, мы дали определения элементарных логических операций. Они позволяют строить сложные (составные) высказывания на основе заданных высказываний.
| |
| Пусть x 1, x 2, x 3, x 4 - переменные высказывания (логические переменные), тогда следующие высказывания:
| |
| 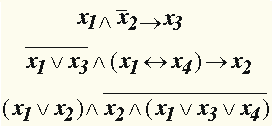 , ,
| |
| представляют формулы алгебры высказываний.
| | 27.
| Так же, как и в алгебре арифметики, в алгебре логики устанавливается приоритет выполнения логических операций. Они упорядочены в следующей последовательности:
| |
| 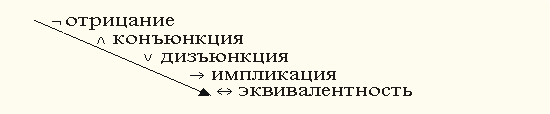 , ,
| |
| При этом отрицание является наиболее сильной операцией, эквивалентность - самой слабой. С учетом указанного порядка две формулы:
| |
|
| |
| и
| |
| имеют одинаковые значения.
| | 28.
| Истинность составных высказываний (логических формул), образованных в результате выполнения логических операций над простыми высказываниями, зависит от истинности исходных высказываний. Для того, чтобы иметь возможность вычислять значения истинности этих высказываний, определим базовое понятие - логическую функцию.
| |
ЛОГИЧЕСКИЕ ФУНКЦИИ |
|---|
| 29. |
Логической функцией называется функция f (x 1, x 1,...,x n) , которая, так же как и ее аргументы, может принимать только два значения (0 и 1). |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30. |
Совокупность значений аргументов будем называть набором . Каждому набору присваивается номер N , равный двоичному числу, образованному значениями аргументов на этом наборе. Условимся, что младшему разряду этого числа соответствует значение аргумента со старшим индексом, и наоборот. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
Итак: |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
Например, пусть логическая функция зависит от трех переменных f(x1,x2,x3). Тогда набор x1=1, x2=1, x3=0 будет иметь номер |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31. |
Любую логическую функцию можно задать таблицей истинности, в левой части которой вписаны все возможные наборы значений ее аргументов x1,x2,...,xn , а правая часть - столбец значений функции, соответствующих этим наборам: |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
Число строк таблицы равно 2n (число всех возможных наборов из n аргументов). Число различных функций n переменных равно 2 в степени 2n - числу возможных расстановок нулей и единиц в столбце с 2n строками. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32. |
Пусть n = 1. Таблица f(x) содержит две строки, а самих функций - четыре. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
| | 33.
| Для n = 2 таких функций f(x1, x2) шестнадцать. Наиболее употребляемые из них:
| |
|
| |
|
| |
|
| | 34.
| Числовой способ задания логической функции. Логическую функцию от n аргументов будем еще обозначать символом f n . Если к тому же известно, что она равна 1 на наборах с номерами a i, i = 0,1,...,2 n-1 , то будем записывать это в виде:
| |
| 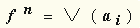 . .
| |
| Например, для функции "Штрих Шеффера" 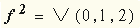 . .
| | 35.
| Если известно, что f n равна 0 на наборах с номерами b i, i = 0,1,...,2 n-1 , то будем записывать это в виде:
| |
| 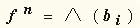 . .
| |
| Например, для " Стрелки Пирса " 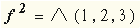 . .
| | 36.
| Аргументы (переменные) и булевы функции с определенными на них элементарными операциями "отрицание", "конъюнкция" и "дизъюнкция" образуют алгебру Буля (булеву алгебру).
| | 37.
| В этой алгебре справедливы следующие основные соотношения, тождества, правила и законы.
| |
|
| |
|
| |
|
| |
|
| |
| а) правило де Моргана: 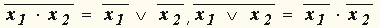 б) конъюнктивное поглощение (x 1 поглощает x 1 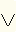 x 2): x 2):
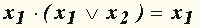
в) дизъюнктивное поглощение (x 1 поглощает x 1· x 2); 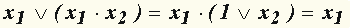
г) конъюнктивное склеивание по x 2: 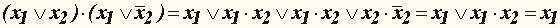
д) дизъюнктивное склеивание по x 2: 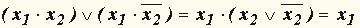 ; ;
е) конъюнктивное развертывание по x 2: 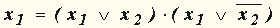 ; ;
ж) дизъюнктивное развертывание по x 2: 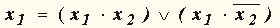 . .
а) ассоциативность дизъюнкции и конъюнкции: 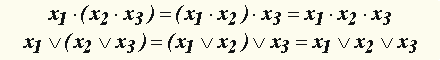 , ,
б) коммутативность дизъюнкции и конъюнкции:
в) дистрибутивность конъюнкции относительно дизъюнкции: 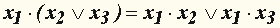 ; ;
г) дистрибутивность дизъюнкции относительно конъюнкции: 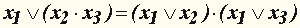 . .
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
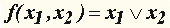
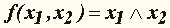
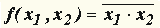
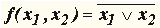
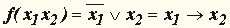
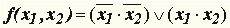 или
x1 -> x2,
или
x1 -> x2,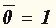 ,
,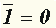 .
.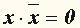 ,
,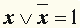
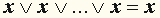 ,
,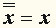 .
.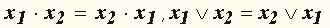
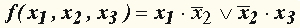 Необходимо построить ее таблицу истинности.
Необходимо построить ее таблицу истинности.
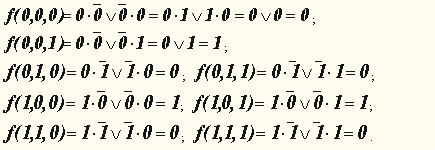
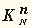 , где
N
- номер конституенты, равный номеру набора, на котором она равна 1.
, где
N
- номер конституенты, равный номеру набора, на котором она равна 1.
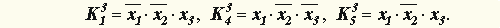 .
.
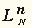 , где N - номер конституенты, равный номеру набора, на котором она равна 0.
, где N - номер конституенты, равный номеру набора, на котором она равна 0.
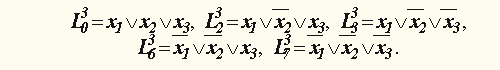
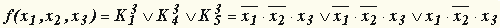 .
.
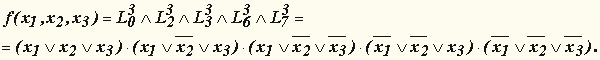
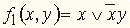 , а
, а
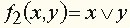 .
.
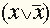 - логическую единицу:
- логическую единицу:
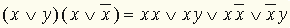
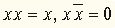 , правилом дизъюнктивного поглощения
, правилом дизъюнктивного поглощения
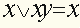 . Окончательно получим:
. Окончательно получим:
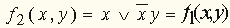
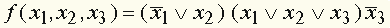
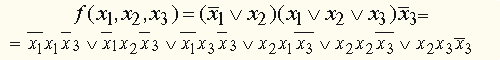
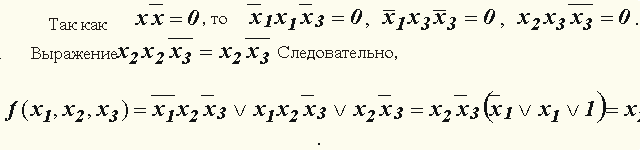
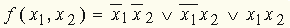
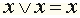 , получим:
, получим:
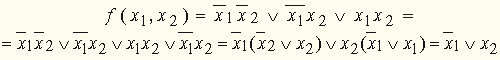
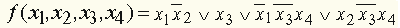
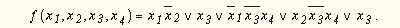
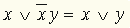 (смотри пример 9), получим:
(смотри пример 9), получим:
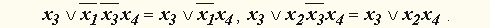
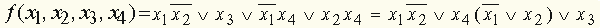
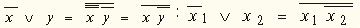
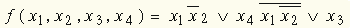
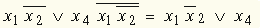
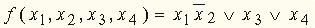
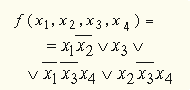
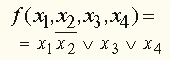
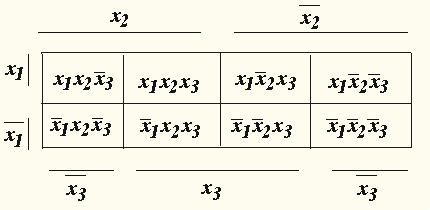
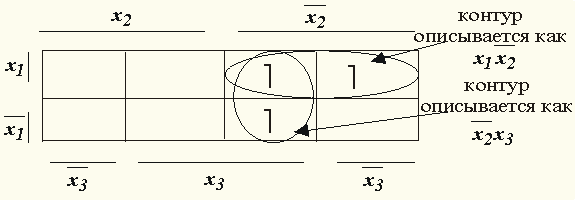
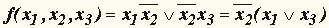
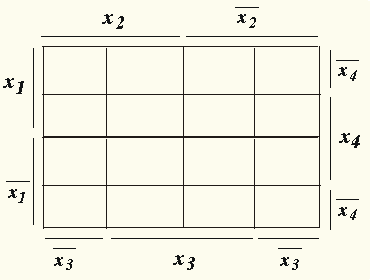
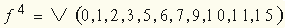
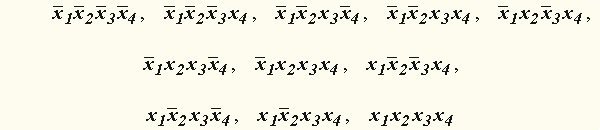
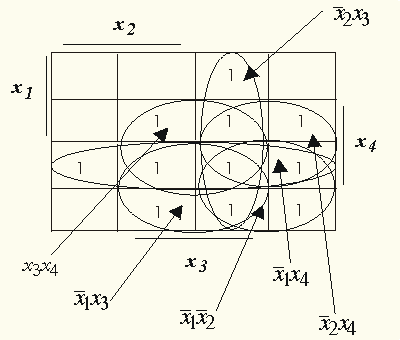
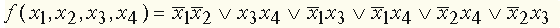 .
.
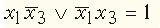
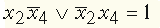
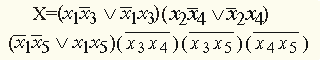
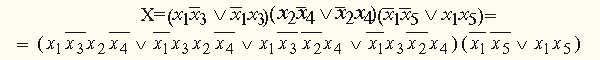
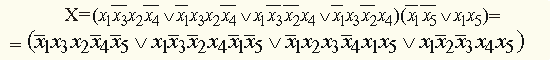
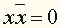 и
и
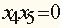 , окончательно получим:
, окончательно получим:
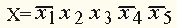
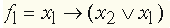 (Импликация - "если : то").
(Импликация - "если : то").
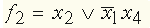
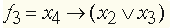
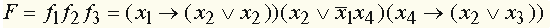
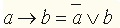 :
:
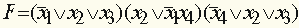 .
.
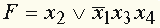
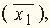 убийство произошло после полуночи (
х4).
убийство произошло после полуночи (
х4).
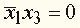 ("Трезвый Франсуа не лжет"), то
("Трезвый Франсуа не лжет"), то
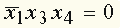 .
.